Encryption to the Future (the math)
Preliminaries
Identity Based Encryption
EtF uses the Boneh-Franklin IBE scheme with type 3 pairings. In brief, identity based encryption is a scheme were a message can be encrypted for an arbitrary string, rather than some specific public key. For example, a message could be encrypted for “bob@encryptme.com” so that only the owner of the identity “bob@encryptme.com” is able to decrypt the message. The BF-IBE consists of four PPT algorithms (Setup, Extract, Encrypt, Decrypt). In brief, these can be defined as:
- \(Setup(1^\lambda) \to (pp, mk)\) where \(\lambda\) is the security parameter, \(pp\) is the output (system) params and \(mk\) is the master key.
- \(Extract(mk, ID) \to sk_{ID}\) outputs the private key for \(ID\).
- \(Encrypt(pp, ID, m) \to ct\) outputs the ciphertext \(ct\) for any message \(m \in {0, 1}^*\).
- \(Decrypt(sk_{ID}, ct) \to m\) outputs the decrytped message \(m\)
DLEQ Proofs
EtF uses DLEQ proofs to verify the correctness of slot secrets without exposing the master secret for the IBE. In brief, the DLEQ proof allows a prover to construct a proof that two group elements were calculated from the same secret (e.g. xH and xG were calculated from the same x) without exposing the secret. Our scheme uses DLEQ proofs to leak an IBE slot secret \(d = sQ\) without exposing the master key, s.
The prover and verifier agree on two group generators, G and H and makes xG and xH publicly known. The goal is for the prover to demonstrate they know xG and xH were derived from the same x.
First, the prover:
- chooses a random \(r \in Z_p\) and calculates \(R1 = rG, R2 = rH\).
- calculates the challenge value with a hash function \(c = H(R1, R2, xG, xH)\)
- calculates the proof of knowledge \(s = r + c* x\)
- shares \((R1, R2, s)\)
With the agreed upon public parameters \(G, H\) and the proof \((R1, R2, s)\), a verifier can be convinced that the prover knows \(x\) without revealing it. The verifier:
- calculates the challenge value by hashing \(c = H(R1, R2, xG, xH)\)
- checks if \(c(xG) - sG == R1 && c(xH) - sH == R2\). If both equalities are true, the proof is valid. otherwise, it is invalid.
Timelock Encryption with ETF Network
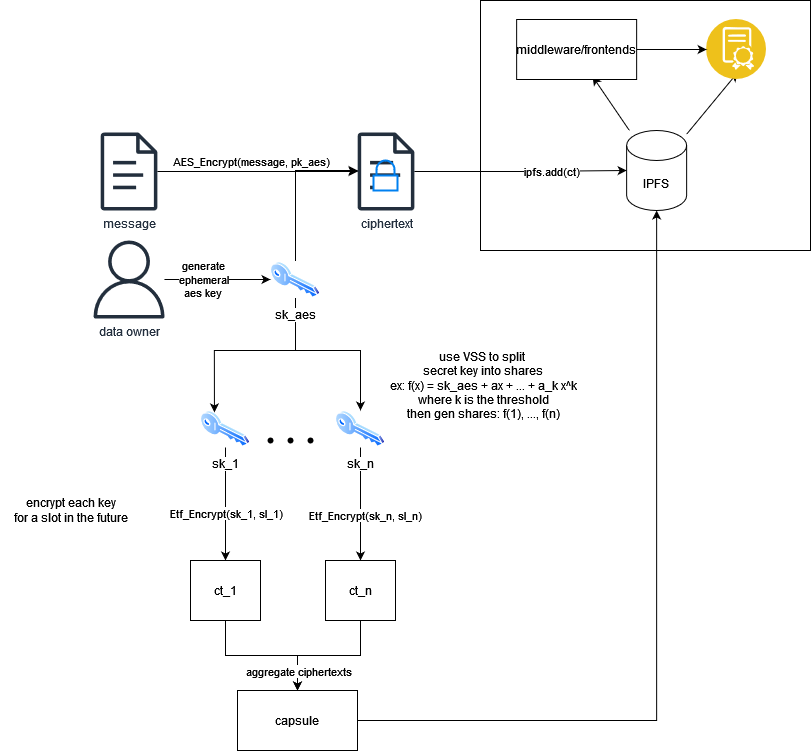
The encryption to the future (EtF) scheme consists of two PPT algorithms, \((Enc, Dec)\), such that:
- \( (f(x), nonce) \leftarrow Setup(k, n) \) for some k < n, and where f(x) is an n degree polynomial. the nonce is a 12 bit nonce for AES.
- \( (ct, capsule) \leftarrow Enc(m, {id_1, …, id_m}) \) for some slot identities \(sl_1, …, sl_m\) and a message \(m \in {0, 1}^*\). It outputs the AES ciphertext \(ct\) and IBE ciphertexts \( capsule = { ct_i = IBE.Encrypt(pp, id_i, f(i)) } \) where \(pp\) is the IBE public parameter.
- \(m’ \leftarrow Dec((ct, capsule), {sk_1, …, sk_m})\) where \(sk_i\) is the secret key leaked in the block authored in the slot with id \(id_i\).
By using IBE and DLEQ proofs, slot winners calculate a proof of knowledge of the master secret along with the derived slot secret, which they include in each block header. Block importers validate the DLEQ proof when importing blocks, ensuring that secrets are only included when they are provably valid.